De hiervoor besproken methode van optimaal nul stellen is de praktische en handmatige manier om de eigenschappen van de luchtbuks te doorgronden en om de buks uiteindelijk optimaal in te stellen. Er is ook een theoretische aanpak, waarbij je met wiskunde en rekenen je luchtbuks kunt doorgronden.
De theorie van kogelbanen is een belangrijke natuurkundige toepassing, die in militaire kringen al sinds mensenheugenis wordt toegepast. Denk aan de baan van een kei uit de katapult van de middeleeuwse ridders, een pijl uit de boog van Robin Hood, een granaat uit een kanon of een ballistische raket met kernkoppen. Voor dergelijke projectielen zijn in de loop van de tijd steeds nauwkeuriger algoritmen ontwikkeld, die natuurlijk ook kunnen worden toegepast op de baan van een pellet uit een luchtbuks.
Het rekenen aan kogelbanen hoort tot de meer complexe vormen van wis- en natuurkunde. Het berekenen van een ideale kogelbaan (zonder rekening te houden met de luchtweerstand) is nog wel te doen en dit zijn opgaven, die regelmatig bij VWO-examens terugkomen. Echter de vorm van de pellet en het gedrag daarvan als het door de lucht vliegt zijn nauwelijks in formules te vangen. Dat betekent dat het rekenen aan kogelbanen wordt ondersteunt door metingen die het gedrag van een projectiel beschrijven. De kennis, die hiermee in de loop van de geschiedenis is verzameld laat zich goed “verpakken” in software. Het perfectioneren van de ingebouwde algoritmen en het vaststellen van de normen voor de vorm van pellets laten we graag over aan ingenieurs van fabrikanten en hobbyisten. Met name de richtkijker fabrikant “Hawke Optics” heeft voor de ons als erfschutters fantastische ballistische software ontwikkeld. Deze komt in meerdere varianten. Er is een uitgebreide versie voor de Apple Mac en MS-Windows en een compacte versie voor IPhone en Android-smartphones.
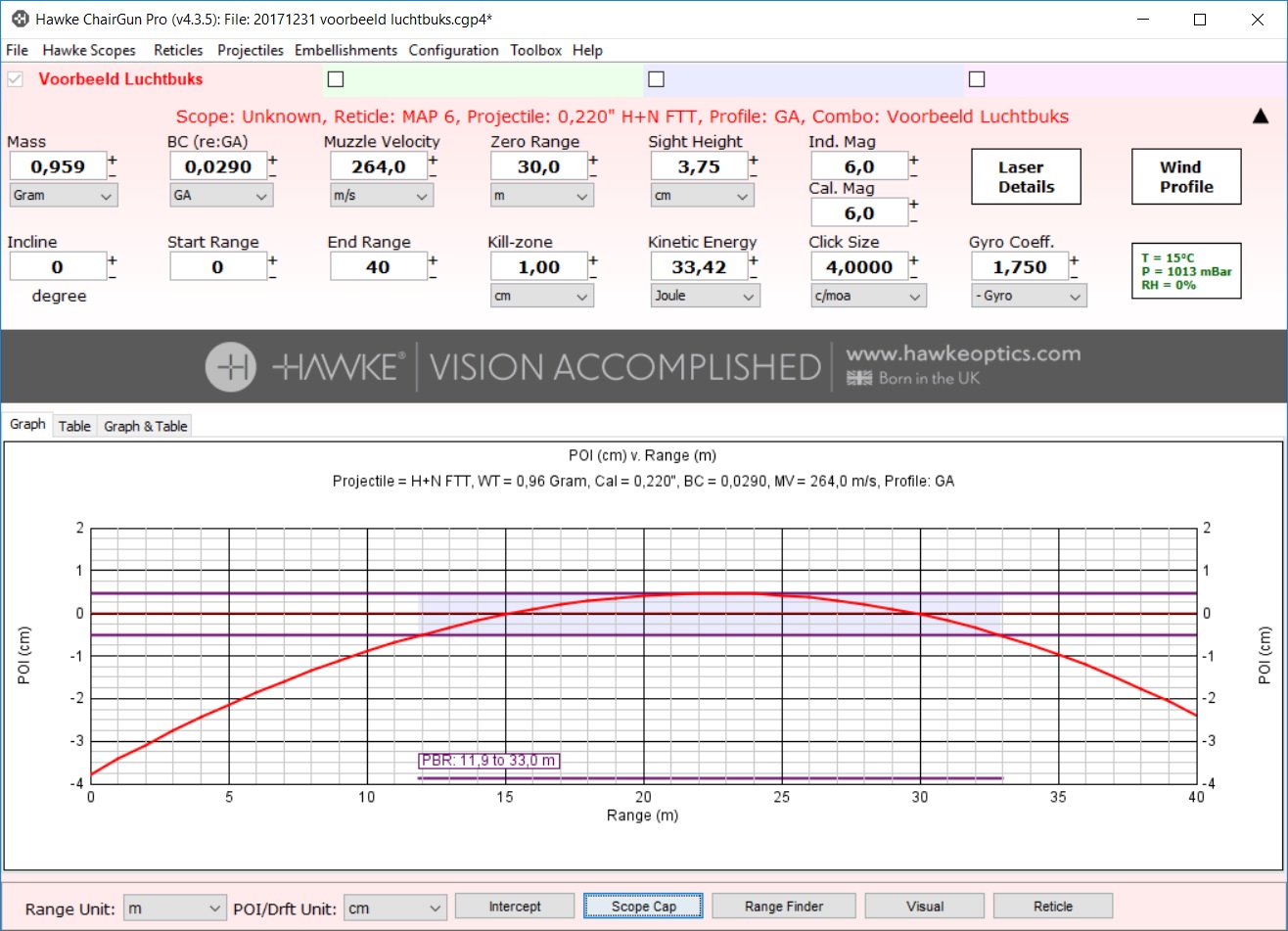
Deze software versie 4.3.5. (zie hierboven) wordt ter beschikking gesteld door Hawke Optics en kan worden gedownload bij www.hawkeoptics.com. Hawke doet dit slim, omdat zij via dit programma hun richtkijkers kunnen promoten. De gangbare modellen Hawke scopes zijn voorgeprogrammeerd in de software. Er komen regelmatig nieuwe versies van deze software uit. Intussen is er ook een versie voor een smartphones. Deze is minder uitgebreid, maar werkt ook erg goed. Om de kogelbaan te kunnen berekenen heb je een paar getallen nodig. Dit zijn:
- de mondingssnelheid in meters/seconde (m/s) of de mondingsenergie in joule,
- het kaliber en gewicht van de pellet,
- het ballistisch coëfficiënt (BC-waarde) van de pellet en het vormfactor (G1 t/m G7, GS, GA etc.)
- de hoogte van de richtkijker boven de loop.
In het volgende bespreken we deze getallen. Kijk ook maar eens naar het volgende filmpje. Dit filmpje is al een paar jaar oud, maar laat goed zien wat er met een persluchtbuks tegenwoordig mogelijk is. Zeker ook door gebruik te maken van Chairgun van Hawke.
Mondingssnelheid of Mondingsenergie
De mondingssnelheid is de snelheid (v) van de pellet als deze de loop verlaat. Op het moment dat de pellet de loop verlaat gaat de pellet vertragen en begint te vallen. De snelheid wordt in meters per seconde (m/s) uitgedrukt. In het schuttersjargon en in de documentatie bij de luchtbuks worden vaak Engelse maten gebruikt. 1 m/s = 3,28 ft/s (feets per seconde).
De mondingsenergie (E) is eerder al aan de orde geweest en deze wordt berekend met de volgende formule E = ½ m v². Voor de voorbeeld-buks is de mondingssnelheid v = 264 m/s. Het gewicht van de voorbeeld-pellet (H&N FTT) m = 0,959 gram.
E = ½ x 0,000959 kg x 264² m/s
E = 33.4 joule
De mondingssnelheid kun je soms moeizaam halen uit de specificaties van de luchtbuks. Leveranciers hebben de neiging de mondingssnelheid voor hun buksen te overdrijven. Vaak wordt een snelheid genoemd op basis van een lichtgewicht kogeltje. Als leveranciers in hun specificaties de mondingsenergie noemen, dan is dit een meer betrouwbaar getal omdat dit onafhankelijk is van de gebruikte pellet. Echter ook de mondingsenergie kan nog behoorlijk variëren. Zelfs voor identieke buksen.
De beste manier om de mondingssnelheid te bepalen is deze gewoon te meten met een chronograaf. Er zijn goedkope versies daarvan (bijvoorbeeld: Combro CB-625 MK4) op de markt die je op de loop kunt plaatsen en die nauwkeurig de snelheid van de pellet meten. De mondingssnelheid van het voorbeeld-luchtbuks met de hieronder genoemde pellet is 264m/s.
Er is ook een chronograaf-App voor Android “Chrono Connect mobile”. Deze toepassing voor smartphones maakt het mogelijk om de mondingssnelheid van uw luchtbuks te meten. Het principe is eenvoudig. De App meet met de microfoon de tijd tussen het schot en de inslag op de doelplaat en berekent dan de snelheid. Het houdt rekening met het gewicht van de pellet, de BC-waarde en de afstand tussen monding en doel. De App is zeker de moeite van het proberen waard. Als je ermee aan de slag gaat moet je ervoor zorgen dat je een doel gebruikt dat veel geluid geeft. Een stuk blik werkt het beste.
Kaliber en gewicht
Het kaliber en het gewicht van de pellet staat doorgaans op het doosje. De BC-waarde vinden was tot nu toe lastig. Echter met de laatste versies van Chairgun komt ook een uitgebreide database met pelletdata.
BC-Waarde en Vormfactor (G1 t/m G7, GS en GA)
De BC-waarde is een getal waarmee de aerodynamische eigenschappen van een projectiel worden weergegeven. Ieder voorwerp ondervindt weerstand als het door de lucht beweegt. De BC-waarde is tegengesteld evenredig aan de weerstand. Een grotere weerstand geeft een kleinere BC-waarde. Deze waarde moet je proberen te vinden bij de leverancier van de pellets. Als dat niet lukt dan kun je op zoek op Internet naar BC-waarden. Over het algemeen zijn de BC-waarden van pellets van bekende merken wel te vinden. Bijvoorbeeld bij Chrono Connect Pellet List. De BC-waarde van de voorbeeld-pellet is “0,029”, het gewicht is 0,959 gram en het kaliber is 5,5 mm of 0.22 inch.
De Vormfactor is een soort filter dat in de berekening wordt meegenomen en dat wordt toegevoegd aan de BC-Waarde. De G1-vormfactor past bij een standaard kogel. Je kunt in de afbeelding zien dat G7 staat voor een heel andere vorm, die zich op zijn vlucht anders gedraagt. Voor diabolo-pellets is de GA-vormfactor gemaakt. Als deze niet beschikbaar is in de ballistische software kun je ook G1 gebruiken.
Hoogte van de richtkijker
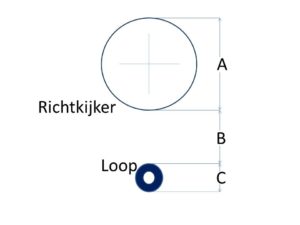Deze hoogte kun je opmeten. Je kunt dat het beste doen door de diameter (A) van de richtkijker te meten (met een schuifmaat), de diameter (C) van de loop en de afstand (B) tussen loop en richtkijker. De hoogte is nu diameter richtkijker (A) gedeeld door twee plus de diameter van de loop (C) gedeeld door twee plus de afstand tussen richtkijker en loop (B).
Hoogte = ½ A + B + ½ C
Voor de voorbeeld-luchtbuks en de Hawke Airmax EV 3-9×40 AO is de hoogte 3,75 cm.
Laat het programma het werk doen…
Als je alle gegevens invoert berekent ChairGun Pro de kogelbaan. Het programma heeft allerlei tools die je kunt gebruiken om bijvoorbeeld de optimale afstand voor kalibreren (OZR) te bepalen. Het werken met Chairgun Pro vereist handigheid met computersoftware en (door de geweldige hoeveelheid functies) de bereidheid om er tijd en energie aan te besteden. Veel functies wijzen zichzelf en voor iedere functie is een helpscherm beschikbaar. Complicatie is dat de software (en de helpschermen) Engelstalig zijn. Als je er niet zelf uitkomt is er op YouTube veel uitleg te vinden.